Module 7 L’enseignant-ressource pour appuyer la diversité en mathématiques et en numératie
Section 4 - Résolution de problèmes
En enseignant par l’entremise de la résolution de problèmes, les enseignants peuvent aider les élèves à aborder de façon autonome de nouvelles situations faisant intervenir les mathématiques. La résolution de problèmes constitue d’abord un objet d’apprentissage de la vie de tous les jours. Au-delà de l’importance des habiletés et des stratégies conduisant à des solutions, elle suppose l’habileté à déceler des problèmes présents dans diverses situations, à construire des modèles de celles-ci et à généraliser ce qui a été élaboré dans l’ensemble du processus.
Important
Lors des résolutions de problèmes, toujours tenir compte du niveau de lecture de l’élève (vocabulaire, images, contexte).
La résolution de problèmes doit aussi apparaitre comme un moyen d’apprentissage, efficace dans l’appropriation et la construction des concepts en tant qu’outils mathématiques.
Qu’est-ce que ça veut dire « enseigner par la résolution de problèmes? »
Pour enseigner par la résolution de problèmes, l’enseignant pose, dès le début du cours, un problème à résoudre; il permet ainsi d’instaurer un contexte qui favorise et justifie l’apprentissage. Cette stratégie se distingue de l’approche traditionnelle qui consiste, notamment, à expliquer une nouvelle procédure, puis à demander aux élèves de résoudre quelques problèmes écrits.
PRIME, 2005
Pourquoi enseigner par l’entremise de la résolution de problèmes?
- Les mathématiques prennent un sens.
- L’enseignant est mieux à même de comprendre la réflexion mathématique d’un élève.
- Les problèmes sont plus motivants quand ils présentent un défi.
- La résolution de problèmes favorise la persévérance.
- La résolution de problèmes permet l’accroissement de l’assurance, l’optimisation de la compréhension et la diversité des styles d’apprentissage et des méthodes.
- Les problèmes sont l’occasion de s’exercer avec les concepts et les habiletés.
- Les élèves s’approprient le sens et la raison d’être des mathématiques.
4.1 Le modèle Polya (1965) comme processus de recherche en résolution de problèmes
Le modèle de recherche de George Polya comprend les quatre étapes suivantes:
Étape 1) Comprendre le problème
Étape 2) Élaborer un plan
Étape 3) Mettre le plan en œuvre
Étape 4) Faire une vérification
Le graphique suivant aide à intégrer ce modèle en salle de classe :
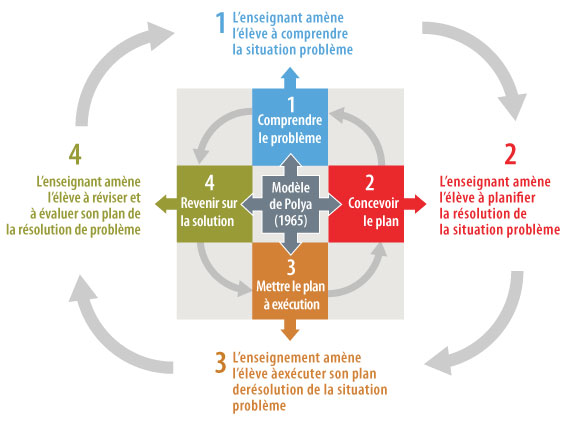
TRANSCRIPTION
Une démarche de résolution de problème basée sur la compréhension
Qu’est-ce que ça veut dire «enseigner par la résolution de problème? »
« Pour enseigner par la résolution de problème, l’enseignant pose, dès le début du cours, un problème à résoudre; il permet ainsi d’instaurer un contexte qui favorise et justifie l’apprentissage. Cette stratégie se distingue de l’approche traditionnelle qui consiste, notamment, à expliquer une nouvelle procédure, puis à demander aux élèves de résoudre quelques problèmes écrits.» Tiré de Connaissances et stratégies, ressource pédagogique pour l’enseignement des mathématiques
Quels sont les avantages d’enseigner par la résolution de problème?
- Donne un sens aux mathématiques, démontre leur utilité et leur mise en application dans la vie
- Permet à un enseignant de mieux comprendre la réflexion mathématique de l’élève
- Plus motivant pour les élèves car ça présente un défi (raisonnable)
- Favorise la persévérance
- Permet l’accroissement de l’assurance et le respect des styles d’apprentissages
- Permet aux élèves de réaliser que faire des math, ce n’est pas seulement d’appliquer des procédures apprises.
- C’est de déployer des efforts pour résoudre un problème
*** Si la résolution de problème est utilisée régulièrement, les élèves deviendront plus autonomes.
Étape 1: Comprendre le problème: J’essaie de comprendre ce qui est demandé
- Est-ce que j’utilise mes stratégies de lecture en lisant mon problème?
- Est-ce qu’il y a des mots que je ne comprends pas?
- Est-ce que je peux imaginer le problème dans ma tête?
- Est-ce que je peux dire le problème dans mes mots?
- Est-ce que j’ai déjà fait un problème comme celui-ci?
- De quelles informations est-ce que j’ai besoin?
- Quelle est la question?
Étape 2: Élaborer un plan: Je décide comment je vais m’y prendre
- Quelle stratégie est-ce que je peux utiliser
- Est-ce que je peux faire un dessin?
- Est-ce que je peux utiliser du matériel concret?
- Est-ce que je peux écrire une équation mathématique?
- Est-ce que je peux trouver une suite ou un tableau?
- Est-ce que je peux utiliser une autre stratégie?
Étape 3: Mettre le plan en oeuvre: Je fais ce que j’ai décidé
- Est-ce que je fais la stratégie que j’ai choisie?
- Est-ce que je laisse toute les traces de mon travail (dessins, mots, symboles…)?
- Est-ce que ma stratégie a du sens?
- Est-ce que je réponds à la question en écrivant les unités (ex: J’ai mangé 5 bonbons)?
Étape 4: Vérifier les résultats: Je vérifie ma solution et je décide si j’ai utilisé une bonne stratégie
- Est-ce que j’ai répondu à la question?
- Est-ce que ma réponse a du sens?
- Est-ce que j’ai vérifié mes calculs?
- Est-ce que ma stratégie était bonne?
- Est-ce que je peux expliquer ma démarche?
Stratégies de lecture pour comprendre un problème
- Voir le problème dans ma tête
- Clarifier le vocabulaire
- Faire des inférences
- Dire le problème dans mes mots
Je vois le problème dans ma tête
Cet été, Daniel et sa petite soeur Sophie iront au parc aquatique avec leurs deux parents. Le coût d’admission est de 3 dollars pour chacun des enfants. Le prix d’entrée d’un adulte est le double de celui d’un enfant.
Quel sera le coût d’admission total pour les quatre membres de la famille?
Je fais des inférences
3 questions à se poser:
- Qu’est-ce que je cherche?
- Quels sont les indices qui me permettent de faire un lien avec la question?
- À quoi les indices me font-ils penser?
Qu’est-ce que je cherche?
Quels sont les indices?
À quoi les indices me font-ils penser?
Cet été, Daniel et sa petite soeur Sophie iront au parc aquatique avec leurs deux parents. Le coût d’admission est de 3 dollars pour chacun des enfants. Le prix d’entrée d’un adulte est le double de celui d’un enfant.
Quel sera le coût d’admission total pour les quatre membres de la famille?
Je dis le problème dans mes mots
Deux enfants vont au parc aquatique
avec leurs parents. Ils doivent payer le coût d’entrée, mais les billets des parents sont plus chers. Je dois trouver ce que ça coûtera pour toute la famille pour aller au parc aquatique.
Éduc@Trousse
4.1.2 Stratégies de résolution de problèmes et niveaux de développement (trousse du sens des nombres et des opérations)
TRANSCRIPTION
Niveau 1
- Reproduire par le jeu.
- Se servir de représentations concrètes.
- Dessiner.
- Procéder par essais et erreurs.
Niveau 2
- Chercher une régularité.
Niveau 3
- Écrire une équation.
- Faire un tableau ou un diagramme.
- Résoudre un problème plus simple.
Niveau 4
- Envisager toutes les possibilités.
- Penser aux cas particuliers.
- Préparer une liste ordonnée.
- Travailler à rebours.
- Raisonner logiquement.
Niveau 5
- Changer d'optique.
Remarque : Les chapitres 5 des guides Connaissances et Stratégies de chacune des trousses PRIME présentent des exemples de problèmes en lien avec les stratégies associées à chacun des niveaux de développement, et ce, pour les différents domaines mathématiques.
4.1.3 Les tâches ouvertes et les tâches à choix multiples au service de la résolution de problème
Les tâches ouvertes et les tâches à choix multiples sont des exemples d’approches centrées sur la différenciation inclusive.
TRANSCRIPTION
Points essentiels des tâches ouvertes
(parfois appelées « questions ouvertes »)
- Elles conviennent à des élèves de niveaux multiples.
- Elles offrent de nombreuses possibilités de réponses et de stratégies de résolution.
- Elles sont susceptibles d’amener vos élèves à vous étonner.
- Elles proposent les mêmes questions de suivi pour tous.
- Elles permettent aux élèves d’apprendre les uns des autres.
Tâches ouvertes - Exemple 1
Tu dessines une lettre E dont l’aire est d’environ 4 unités carrées. Dessine une autre lettre et estimes-en l’aire.
Référence : Enseignement différencié en mathématiques de Marian Small
Tâches ouvertes - Exemple 2
Complète la phrase suivante à l’aide de fractions :
Julien s’exerce à dessiner. Il remplit _______ page en _________ heure. À ce rythme, combien de pages peut-il remplir en une heure?
Points essentiels des tâches à choix multiples
(parfois appelées « tâches parallèles »)
- Elles comprennent deux tâches analogues (Tâches qui se ressemblent qui est différenciées en terme de complexité.) ou plus, conçues en fonction de différents niveaux de développement.
- Le choix de la tâche à réaliser peut revenir à l’élève ou à l’enseignant.
- Elles sont revues en grand groupe à partir de questions de suivi communes.
- Elles sont susceptibles d’amener vos élèves à vous étonner et à apprendre les uns des autres.
Tâches à choix multiples – Exemple 1
Les deux points ci-contre sont des sommets d’une figure.
Tâche 1 : Construis un carré qui a ces sommets.
Tâche 2 : Construis un parallélogramme qui a ces sommets.
Tâche 3 : Construis un triangle isocèle qui a ces sommets.
Utilise un tangram.
Tâche 1 : Ajoute les pièces de tangram correspondantes.
Tâche 2 : Construis un carré avec cinq pièces de tangram.
Tâche 3 : Construis cette figure.
Éduc-et-Notes
Quelles sont les caractéristiques de chacune de ces deux tâches?
En quoi ces différentes tâches peuvent-elles contribuer à mieux répondre aux besoins de la diversité en salle de classe?